Investigadores de la Universidad Politécnica de Madrid (UPM) han demostrado que las herramientas matemáticas desarrolladas para el modelado y el análisis de sistemas caóticos y complejos no lineales ayudan a conocer el comportamiento y la respuesta del cuerpo humano al ejercicio. Los científicos han desarrollado un modelo para explicar este fenómeno fisiológico y mejorar el rendimiento.
En los años recientes se ha desarrollado un número de técnicas matemáticas para el estudio de fenómenos no lineales como el caos, la bifurcación y la complejidad en diferentes campos de la física, la biología, la ingeniería etc. Con estos métodos se puede estudiar y comprender el comportamiento complejo de estos fenómenos. Estas herramientas tienen también muchas aplicaciones en los campos de medicina, salud y deporte.
Así, el Laboratorio de Análisis de la Actividad Física y del Deporte adscrito a la Facultad de Ciencias de la Actividad Física y del Deporte (INEF) de la Universidad Politécnica de Madrid ha aplicado algunas de estas herramientas a problemas en el deporte y el ejercicio, en concreto, a la respuesta cardíaca al ejercicio. El objetivo ha sido comprender los factores que controlan los mecanismos básicos que afectan al rendimiento y así comprender cómo se puede mejorar el rendimiento.
Y son éstas las mismas herramientas que el grupo ha utilizado previamente para resolver problemas en aplicaciones en otras áreas como la contaminación en flujos, la óptica no lineal, la óptica de sistemas telescópicos y la física de estado sólido.
El ritmo cardiaco se utiliza como indicador para controlar la respuesta del cuerpo a programas de ejercicio y entrenamiento, tanto en el público general como en deportistas de todos los niveles. De igual modo, el ritmo cardiaco se utiliza en medicina ya que proporciona información relevante respecto a la salud de una persona: irregularidades en la señal cardiaca pueden indicar posibles problemas de salud.
El Laboratorio de Análisis de la Actividad Física y del Deporte ha desarrollado un modelo matemático sobre la respuesta cardiaca y la respuesta del ritmo de captación de oxigeno al ejercicio en la forma de un sistema dinámico no lineal, utilizando un conjunto de ecuaciones diferenciales no lineales. El modelo se ajustó a datos experimentales de atletas utilizando métodos de optimización estocástica.
El nuevo modelo se puede utilizar para comprender los mecanismos fisiológicos básicos del cuerpo durante el ejercicio y de esta manera hacer predicciones de la respuesta del cuerpo a ejercicios de diferentes intensidades. Los usos obvios para este modelo son tanto el diseño de sesiones de entrenamiento como las estimaciones de la respuesta del cuerpo a ejercicios de intensidades que no se desean alcanzar durante el ejercicio.
Realizar, por ejemplo, una prueba de esfuerzo máximo no es imposible para una persona mayor, enferma o embarazada. Los resultados de tal prueba pueden, sin embargo, ser muy importantes respecto a la respuesta del cuerpo a tal esfuerzo.
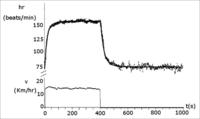
Por otro lado, en el deporte es posible optimizar una sesión de entrenamiento (ver fig.), utilizando nuestro modelo, con el objetivo de maximizar los efectos deseados y de esta manera mejorar el rendimiento de los atletas. El modelo también se puede utilizar para diseñar estratégicas de rendimiento óptimas en competiciones: estudiando la respuesta cardiaca se puede, por ejemplo, diseñar una estratégica optima para una carrera.
Nuestro trabajo se ha llevado a cabo en colaboración con el Instituto de Ciencias Matemáticas, el profesor Bengt Saltin del centro Copenhagen Muscle Research de Dinamarca y la profesora Véronique Billat del Laboratorio de Estudio de la Fisiología del Ejercicio de la Universidad de Evry, Francia.






